李金莲
甘肃省古浪县第一中学 甘肃古浪 733100
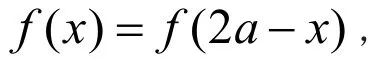

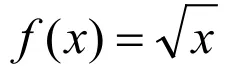
【巧妙解法】因为f(x)=f(2a -x() a ≠0),所以函数f(x)的对称轴为x=a,所以准偶函数的定义等价于:若函数f(x)的图象存在对称轴x = a (a≠0),则称f(x)为准偶函数.
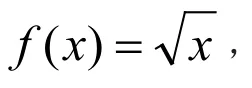
点评:本题以函数图象的对称性的符号语言为背景,考查新定义函数的内容,试题既新颖灵活,又可以考查学生的创新意识和创新能力、数形结合能力,以及运算求解能力,为中档难度题.
【思考1】如果原题中新定义的准偶函数不变,把结论进行变化,将选择题改为填空题,便可得到如下问题,但其难度将提高一个档次.

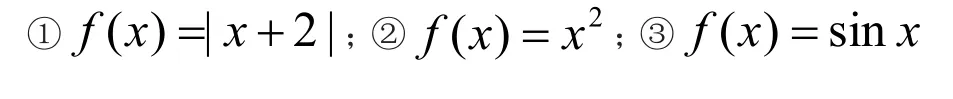

【思考2】如果把原题中的条件“f(x)=f(2a-x)”改为“f(x)=-f(2a-x)”,并把新定义的函数名称“准偶函数”改为“准奇函数”,选择题改为填空题.将得到如下问题.

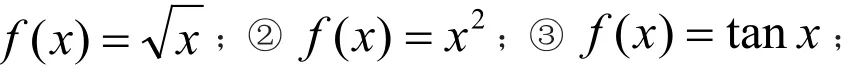
解析:因为f(x)=-f(2a -x() a ≠0),所以函数f(x)的图象关于点(a ,0)对称,所以准奇函数的定义等价于:若函数f(x)的图象关于点(a,0)(a ≠0)对称,则称f(x)为准奇函数.