杜薇 陕西省西安中学 陕西西安 710018
数学建模是数学核心素养之一,将数学建模应用到高中数学教学中,不仅能够调动学生学习的积极性,拉近数学学习和实际生活间的关系,而且还能够锻炼学生在问题分析和解决方面的能力,促进学生学习能力的提升。由此可见,数学建模在高中数学教学中发挥着重要作用。以下通过设计双曲线及其标准方程这节课,来具体说明在上课过程中如何渗透数学建模思想。
课题:双曲线及其标准方程
教学目标:
①知识与技能:理解巧曲线推导过程及掌握其标准方程。
②过程与方法:在教学中,让学生体会到数学建模过程。
③情感态度与价值观:通过这节课,使得学生的空间想象、实践能力及运算能为,同时也提高了同学们对于数学学科的兴趣。
教学重难点:
①重点:掌握并且理解双曲线的标准方程。
②难点:理解建立模型的过程。
教学方法:探究合作法。
教学用具:三角板。
教学过程:
(1)复习
教师提问:椭圆的定义是什么?我们上节课是怎样得到椭圆的方程的?
(注:通过回忆以上的知识和椭圆形成的过程,让学生再次体会数学建模的过程,也为这节课通过数学建模形成双曲线的概念做好铺垫.)
(2)讲授新课
①思考题
两定点的距离差为非零常数的点的轨迹是怎样的曲线呢?
(设置这个问题可以让学生与椭圆的定义形成鲜明的对比,前者是两定点间的距离之和为定值,后者是两定点之间的距离之差为定值,很容易引发学生去积极的思考。)
②动手实践
让同学们拿出来课前事先准备好的教具,让同学们自己动手实践。拿出准备好的教具,把拉链拉开一段,在它拉开的两边分别选择出2个点,将这2个点依次粘在画板上,分别将这2个点记为F1F2将笔尖放在拉链的开口处,将开口处记为M,且M到F1的距离减去M到F2的距离之差为2a,点F1和点F2之间距离为2c,当拉链慢慢的张开和合拢,此时画出的轨迹是一条双曲线。如图:

而且这条曲线满足
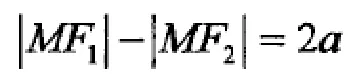
如果使点到距离减去到的距离之差为,我们就可得到另外一条曲线,而送条曲线的满足
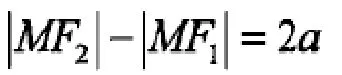
学生做完之后,教师在黒板上演示和几何画板上进行动画演示,让学生对照自己的实验过程,再一次体会双曲线形成的过程。
接下来抽象出双曲线的图形(模型的建立)
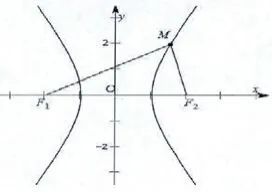
(注:通过以上教学过程,同学们刚开始对双曲线是感性认化然后上升到理性认识,而且将这个实际操作过程转化成一个数学模型,再次可以体会建模的过程。)
(3)双曲线的标准方程
根据以上的实验过程得
① 型的建立
建立如图的直角坐标系,以点F1,点F2所在的直线为x轴,线段F1F2的垂直平分线为y轴,点求:双曲线的标准方程。
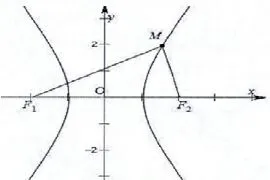
②模型的求解
由已知条件得

(4)例题示范
例 现在有A、B两个侦测所,两个侦测所之间的距离为1000m,远处有一个炮弹暴炸,A侦测所听到的爆炸声比B侦测所听到的爆炸声时间晚了2s,声音的速度为340m/s,求炮弹爆炸点所在的曲线的方程。
解 ①模型建立
建立如图所示的直角坐标系,以A,B两点的所在的直线为x轴,以线段AB的中点O为原点建立直角坐标系,已知,点M是爆炸点,求点M所在的方程。


小结:以上就是与双曲线有关的建模案例,首先通过认真分析题目,再建立适当的数学模型,发现可以归为双曲线的问题,最后进行求解。对于学生来说,将应用题转化为数学问题还是有一定难度的,教师在引导学生做这类题目的时候,应该首先带领同学们读题目想表达的意思,再慢慢引导学生将应用题抽象成与数学有关的问题,也就是建模的过程,这个过程是非常重要的。
(5)总结:通过设计双曲线的定义的推导过程,让学生体会对待事物的感性认识要上升到理性认识,也就是从实验过程得到双曲线的准确定义的过程。最后,通过推导双曲线的标准方程的过程和例题的讲解,让学生体会如何将一个应用题抽象为数学问题,其实也就是了解建模的过程。
数学建模的应用在高中数学教学阶段是非常必要的,数学教师应该在教学过程中重视和培养学生在建模方面的能力,让学生能够从题目的数据和变量关系中快速找到问题解决方向,并且利用合适的建模方法建立相应的数学模型,解决问题,不断提升学生数学核心素养,培养学生在问题分析和解决方面的能力,推动高中数学教学的发展。



















