陈泳红 长沙街道办事处谭宏帙纪念小学 529300
数形结合作为数学教学中的一种重要的思想方法.它既具有数学学科的鲜明特点,又是数学研究的常用方法。用“数”分析“形”,会使“形”更加精彩,更加数量化:用“形”表示“数”,会使“数”更加形象,更加直观化。我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。”因此,“数形结合”思想正是数学思想方法的有力体现,它使教与学收到事半功倍之效。
一、数形结合,提升教学效益
教师有意识地运用数形结合思想进行教学设计,化抽象为形象,创造性地开发课程资源,有效地提升教学效益。我们教研组在备《乘法分配律》这节课时,教师很好地借助数形结合,拼摆图形,让学生感知乘法分配律的模式,让学生知道在数学的领域里,同一个结果,存在分开算和合起来算的方法,但必须是两个数的和乘一个因数,才可以先把这两个数分开与这个因数相乘,再相加。而这个因数用苹果来代替,学生很容易的就找出相同因数来,再分开一个加数一个。或者把两个加数加起来,再乘苹果。教师板书(30+25)×=30×+25×,数形结合,学生很形象的初步建立乘法分配律的模式。
二、数形结合,降低教学难度
(1)借助数形结合,使复杂内容简单化。在数学教学中教师要有意识地利用数形结合进行教学,将复杂的问题通过图示简单化、明朗化,逐步帮助学生建立起数形结合的思想,培养其主动运用数形结合的方法去解题的意识,长期坚持训练,内化数形结合思想,成为运用自如的思想方法和思维工具,从而提高学生数学思想与解题能力,降低教学的难度,让学生乐学。例如在教学乘法结合律的时候,笔者利用数形结合法,通过摆一摆,拼一拼小正方体,求大的长方形里包含几个小正方形。
这样很好地借助形象模型进行直观思考,放手让学生去探索规律并想办法予以确认,这样不仅充分激发了学生学习的积极性,而且使学生体会了发现新规律的方法。这一大环节中让学生在自己的探索中学习,体现自主、合作的学习方式 。借助数形结合,使复杂内容简单化
(2)指导学生运用数形结合思想解题
笔者在教学的过程中发现有个别的学生他们把乘法分配律和交换律、结合律混为一谈,张冠李戴,错漏百出。原因是很多孩子对乘法分配律都是死记硬背,在实际练习中,他们又经常丢三落四,没有将数形结合起来,所以教给学生数形结合的方法尤其重要。
在解题中,当学生遇到困难无从下手时,要求学生通过画线段图或示意图理解题意,部分同学不能选择怡当的图示清楚的表示出题意,这时教师可指导学生怎样清楚的运用图形表达题意,从而在图形上直观的分析数据,把握解決题目的最佳方法。
(3)在比较中体会数形结合的优势。
数形结合思想在教学中应用可以降低教学的难度,让学生的数学素养得到提升,让运算定律变得易学。在解决同一问题中,将学生的不同解题方法进行对比,让学生在对比反思中体会,运用图形帮助解题,很多问题便迎刃而解,且解法简捷,起到事半功倍的作用。
三、数形结合,取得双赢局面
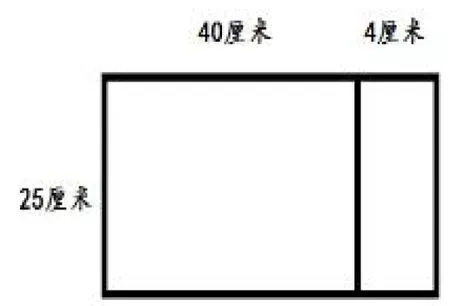
1.数形结合,解决难点对于后进生光靠讲解来理解运算律算理比较抽象。教师可借助“数形结合”思想解决难点。如针对学生在运用乘法分配律时中常“漏乘”的现象:25×(40+4)=25×40+4,可引导学生看着下图求大长方形的面积,借助图形帮助学生分析求出的不是大长方形的面积,而是左边长方形的面积加上1条宽的长度,无意义。这样借助图形帮助学生思考数与数之间的关系,有助于发展学生的形象思维,有效避免类似的错误再次发生。
2.清晰算理,以理驭法
面对灵活多样的变式题,教师应让学生去寻找它的意义本源,寻找这些特例与运算定律之间的内在联系,然后重新组建新的认知结构。让学生说算理是一种比较好的教学方法,还能起到举反三的效果。
如教师以乘法分配律的基本公式为基础,进行变式,并将一些易混淆的题目组成题组,通过对比让学生掌握本质。学生容易出现错误:
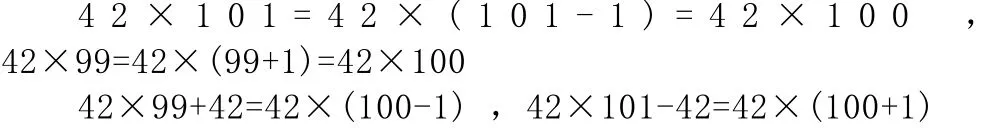
学生只想到凑整,却不会考虑变化的数目及变化前后是否相等。此时教师可引导学生把“42×101”与“42×99”进行对比:“42×101”表示101个42是多少,可以先算100个42是4200,在加上1个42就是4242:“42×99”表示42个99是多少,可以先算100个42是4200,再减去1个42,得到4158。这样既进行了算式意义上的区分,又在内涵上架起了原式与乘法分配律的内在联系“42×99+42和42×101-42同样如此教学。
“数形结合”对教师来说是一种教学策略;学生来说是一种学习方法。通过本课题的实践,提高学生应用数形结合思想解决实际问题的能力,使学生形成良好的数学意识,从而提升学生的思维水平,激活运算定律教与学的思维模式。只有这样的教学才扎实有效,真正实现教与学的双赢局面。


















