王浩
(江苏省海安高级中学,江苏南通 226500)
1 背景
函数构造论是数学分析的一个分支,起源于数学家切比雪夫的伟大工作:内插理论,机械求积,矩量问题。它所研究的是利用简单的分析工具来研究近似表达任意函数的问题。在函数的一致逼近理论中,我们遇到过一种问题:能不能用多项式去逼近一个任意给定的函数,并且具备已给定的精度。1885年Weierstrass第一定理给我们指出,闭区间上的连续函数可以用多项式来表示并具有预先给定的精度。然而,这样给出的多项式次数可能很高。自然要问:如果预先对多项式的次数进行限制,那么能达到什么样的精度?这就是切比雪夫逼近。在中学数学解题中,我们会经常遇到一类带绝对值的含参函数f(x)-Ax-B求最大值的最小值问题,其本质是用直线y=Ax+B对函数f(x)进行切比雪夫逼近,即求f(x)的一次最小偏差多项式。2 切比雪夫逼近理论简介
我们用H表示一次多项式的集合,C[a,b]表示闭区间[a,b]上连续函数的集合。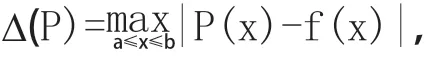
(2)若x∈[a,b],使得P(x)-f(x)=E(f),则x称为(+)点,若P(x)-f(x)=-E(f),则x称为(-)点。
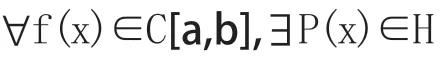
定理2:(+)与(-)都存在。
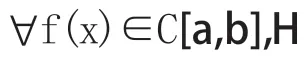
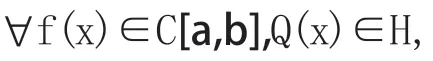
定理5:若函数f(x)在闭区间上有不变号的二阶导数,则f(x)的最佳逼近直线为:
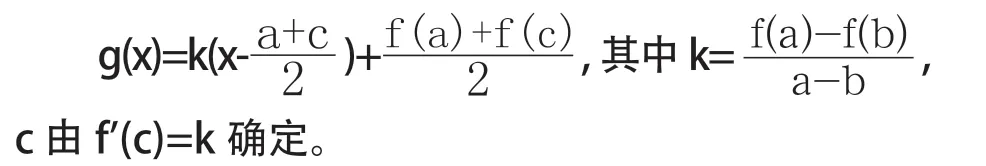
几何意义:g(x)实际上就是函数f(x)在闭区间[a,b]的极值点和函数f(x)图像的两个端点连成的两条线段的中点所在的直线。
3 解题应用

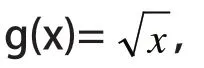
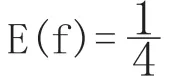
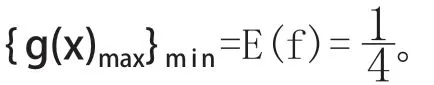

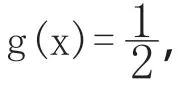
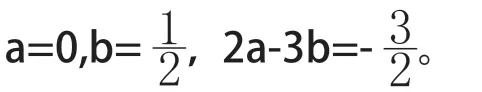
例题3:f(x)=|x-ax-b|,x∈[-1,1],f(x)的最大值为M[a,b],求M[a,b]的最小值。
解析:令p(x)=x,p(x)=6x,由于p(x)二阶导数在区间[-1,1]上变号,因此不能直接利用定理5的结果,我们考虑一次最佳逼近的几何意义,发现最佳逼近直线就是两条夹逼区间内图像的直线的中线。
如图1所示,分别过图形的两个端点A,C求出切线,易得切线分别为:3x-4y+1=0,3x-4y-1=0。所以最佳逼近直线为3x-4y=0。
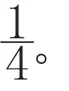
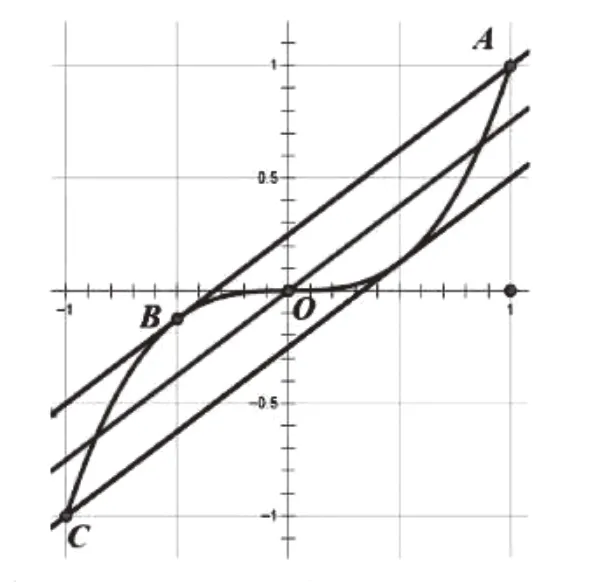
图1 解题图
例题4:已知f(x)=acosx-4cosx,若对任意的x∈R,都有|f(x)|≤1,求a的值。
解析:令cosx=t∈[-1,1],则函数f(x)=at-4t,类似于例题3,可以求出最佳逼近直线为y=3t, 所以a=3。
4 思考与感悟
函数是描述客观世界变化规律的主要模型,函数的变化特征反应了自然规律的变化特征。研究函数就是要研究数量之间的相互关系。函数的内容丰富,我们可以从不同的角度研究,比如单调性、奇偶性、周期性。函数题目灵活多变,主要考察学生对性质的整体把控,以及对性质的进一步研究。本文通过对利用切比雪夫一次逼近解题的研究,笔者得到一些启发。对于求最大值的最小值问题我们可以从切比雪夫逼近的角度挖掘问题的本质,关注几何和代数的联系,转化其中解题的通性通法。通过对问题的转化、变换,可以激发学生对数学的兴趣,同时培养学生思维的广阔性。高考数学突出考察学生的基础知识、基本技能、基本思想和基本活动经验,而这其中多学生的基本思想考察尤为重视。转化思想、数学结合的思想在考题中都有很充分的体现。我们要教会学生从“形”和“数”两方面来思考问题。数学教学的核心是要突出主体性和思维性。学生的思维广度和深度的提高、解题能力的提升、对于数学的认识的加深都是自身逐步内化的过程。我们在教学过程中既要精准施教也要注意培养学生进一步探究的能力。


















